EQUAZIONE DELLA RETTA PASSANTE PER DUE PUNTI: ESERCIZI
Dopo aver visto, nella lezione precedente, qual è l'EQUAZIONE DELLA RETTA passante per DUE PUNTI, in questa lezione vogliamo vedere alcune applicazioni pratiche.
Esempio 1:
Scrivere l'equazione della retta passante per i punti
P0 (1 ; -1) e P1 (3 ; 5).
Applichiamo la formula:
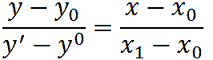
Sappiamo che:
x0 = 1
y0 = -1
x1 = 3
y1 = 5.
Sostituendo otteniamo
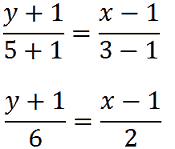
Ora, eliminiamo i denominatori moltiplicando, entrambi i membri, per 6:
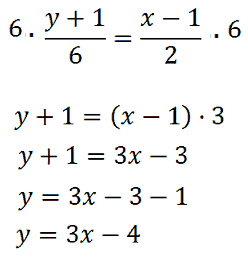
Abbiamo così ottenuto l'equazione della retta da noi cercata.
Per sicurezza vogliamo verificare che essa passi veramente per i punti P0 e P1. Per farlo proviamo a sostituire all'equazione, il valore dell' ascissa del punto P0 e vediamo se otteniamo la sua ordinata e, successivamente facciamo la stessa cosa con il punto P1.
| x | y |
|---|---|
| 1 | -1 |
| 3 | 5 |
Dunque abbiamo trovato esattamente la retta cercata.
Esempio 2:
Scrivere l'equazione della retta passante per i punti
P0 (2 ; 3) e P1 (-2 ; -1).
Applichiamo la formula:
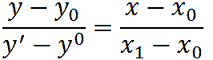
Sappiamo che:
x0 = 2
y0 = 3
x1 = -2
y1 = -1.
Sostituendo otteniamo
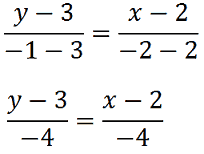
Ora, eliminiamo i denominatori moltiplicando, entrambi i membri, per -4:
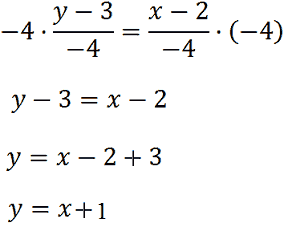
Abbiamo così ottenuto l'equazione della retta da noi cercata.
Anche in questo caso, per sicurezza vogliamo verificare che essa passi veramente per i punti P0 e P1.
| x | y |
|---|---|
| 2 | 3 |
| -2 | -1 |
La retta trovata è esattamente quella cercata.
Esempio 3:
Calcolare il coefficiente angolare della retta passante per i punti
P0 (2 ; -2) e P1 (1 ; -4).
In questo caso non ci viene chiesto di scrivere l'equazione della retta passante per i due punti, ma semplicemente di calcolare il coefficiente angolare di tale retta. Certo, noi potremmo scrivere tale equazione e, da essa, ricavare il coefficiente angolare, ma possiamo anche calcolare direttamente tale coefficiente.
Infatti, nella lezione precedente, abbiamo appreso che
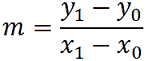
Noi sappiamo che:
x0 = 2
y0 = -2
x1 = 1
y1 = -4.
Sostituendo otteniamo
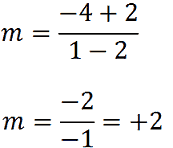
Ora proviamo a fare una verifica. Scriviamo l'equazione della retta passante per i due punti e verifichiamo che il coefficiente angolare sia esattamente quello da noi trovato. Applichiamo la nostra solita formula:
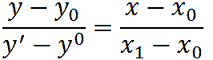
ed effettuiamo le sostituzioni
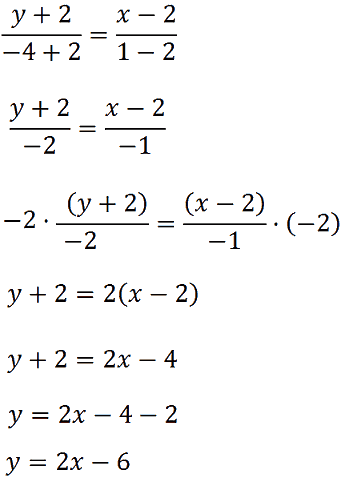
Chiaramente il coefficiente angolare è 2.






