INSIEMI DEI NUMERI N, Z, Q, R
- L'insieme dei numeri naturali
- L'insieme dei numeri interi relativi
- L'insieme dei numeri razionali relativi
- L'insieme dei numeri reali
- Operazioni nei numeri naturali
- Operazioni nei numeri interi
- Operazioni con i numeri razionali
- Insieme Q: insieme discontinuo
- Rappresentazione grafica di un insieme
Nelle lezioni precedenti abbiamo parlato dell'insieme dei NUMERI NATURALI, dell'insieme dei NUMERI INTERI, dell'insieme dei NUMERI RAZIONALI e dell'insieme dei NUMERI REALI.
Abbiamo detto che la sottrazione e la divisione non sono operazioni interne in N.
Per superare queste limitazioni sono stati introdotti:
- l'insieme dei numeri interi Z;
- l'insieme dei numeri razionali Q.
I numeri interi sono i numeri positivi e negativi. I numeri positivi non sono altro che i numeri naturali. Per questa ragione abbiamo detto che l'insieme N è un sottoinsieme di Z.
La sottrazione è un'operazione interna in Z. Mentre la divisione non sempre è eseguibile tra i numeri interi.
I numeri razionali Q sono le frazioni. Poiché anche i numeri interi possono essere espressi sotto forma di frazioni possiamo dire che l'insieme Z è un sottoinsieme di Q.
La divisione è un'operazione interna in Q.
I numeri razionali comprendono:
- i numeri decimali limitati;
- i numeri decimali periodici.
Ogni numero razionale corrisponde ad un punto di una retta orientata, ma non tutti i punti della retta indicano un numero razionale. Per superare questa limitazione sono stati introdotti i numeri reali.
L'insieme dei numeri reali R comprende sia i numeri razionali che i numeri irrazionali, ovvero i numeri decimali illimitati. Poiché R comprende anche i numeri razionali possiamo dire che Q è un sottoinsieme di R.
In altre parole:

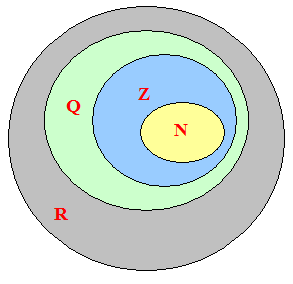
Ecco, allora, come possiamo rappresentare i nostri insiemi con i diagrammi di Eulero-Venn: