RISOLUZIONE DELLE EQUAZIONI ESPONENZIALI CON METODO GRAFICO
- Funzione esponenziale
- Risoluzione delle equazioni di secondo grado complete
- Risoluzione di equazioni esponenziali
- Equazione esponenziale elementare
- Risoluzione di equazioni esponenziali con potenze della stessa base
- Risoluzione di equazioni esponenziali con potenze aventi lo stesso esponente
- Risoluzione di equazioni esponenziali con potenze aventi basi ed esponenti diversi
- Risoluzione delle equazioni esponenziali mediante sostituzione
Concludiamo l'esame dei metodi di risoluzione delle EQUAZIONI ESPONENZIALI esaminando quelle equazioni nelle quali l'INCOGNITA NON compare solamente ad ESPONENTE.
Stiamo parlando di equazioni esponenziali che si presentano in questa forma
af(x) = g(x)
o di equazioni che, pur non presentandosi in questa forma, possono essere ricondotte ad essa.
Questo tipo di equazioni può essere risolta solamente usando il METODO GRAFICO: si tratta di un metodo che non ci permette di ottenere un risultato esatto, ma solamente un risultato APPROSSIMATIVO.
Vediamo in cosa consiste questo metodo.
Si tratta di scrivere due funzioni, una per ognuno dei membri della nostra equazione. Le due funzioni saranno:
y = af(x)
e
y' = gf(x).
In altre parole scriveremo la nostra equazione come un sistema di due funzioni:
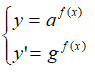
Quindi si dovrà procedere a DISEGNARE i GRAFICI di esse.
Le ASCISSE dei PUNTI di INTERSEZIONE delle due funzioni saranno le SOLUZIONI della nostra equazione.
Qualora le due funzioni non si intersecano significa che l'equazione di partenza non ammette soluzioni.
Esempio:
3x - 1 = x + 2.
La prima cosa da fare è scrivere il sistema
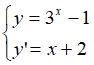
Ora andiamo a disegnare i grafici delle due funzioni. Lo facciamo attribuendo alcuni valori alla x e cercando i corrispondenti valori delle y. Partiamo dalla prima funzione:
y = 3x -1
| x | y |
|---|---|
| -2 | -8/9 |
| -1 | -2/3 |
| 0 | 0 |
| 1 | 2 |
y'
= x + 2
| x | y |
|---|---|
| -2 | 0 |
| -1 | 1 |
| 0 | 2 |
Il grafico delle due funzioni è il seguente:
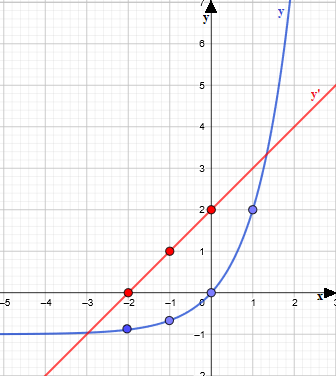
Ora cerchiamo i loro punti di intersezione:
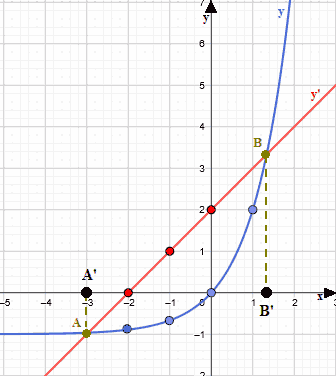
Abbiamo indicato i due punti con le lettere A e B: le ascisse di questi due punti, individuate nel grafico dalle lettere A' e B' sono le due soluzioni dell'equazione data.






