ANGOLI E QUADRANTI
Disegniamo una CIRCONFERENZA GONIOMETRICA
Ora, disegniamo l'ANGOLO ORIENTATO α:
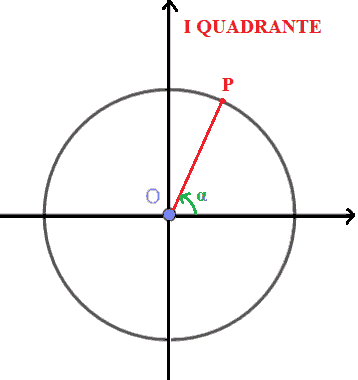
Il punto P, associato all'angolo α, si trova nel primo quadrante, quindi diremo che α è un ANGOLO del PRIMO QUADRANTE
E' evidente che il punto P è associato anche all'angolo:
α + 360°
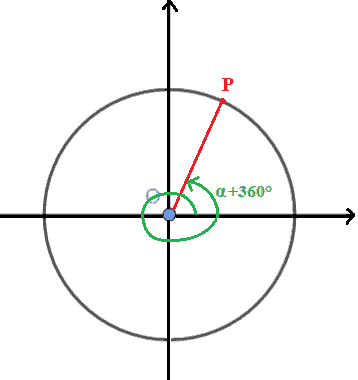
Come pure tale punto è associato all'angolo:
α + 360° + 360°
E' chiaro, quindi, che anche questi angoli sono angoli del primo quadrante.
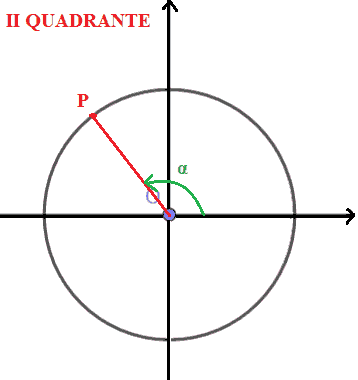
Se il punto P si trova nel secondo quadrante, diremo che l'angolo α è un ANGOLO del SECONDO QUADRANTE
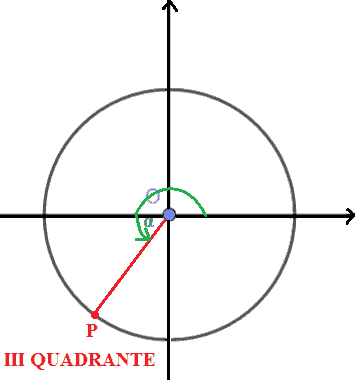
Se, invece, il punto P si trova nel terzo quadrante, diremo che l'angolo α è un ANGOLO del TERZO QUADRANTE
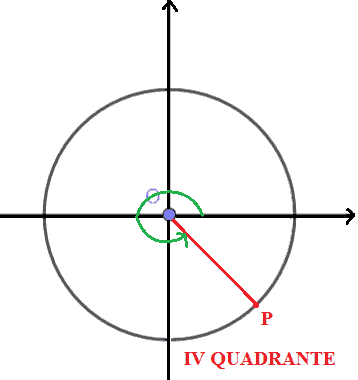
Ed infine, se il punto P si trova nel quarto quadrante, diremo che l'angolo α è un ANGOLO del QUARTO QUADRANTE
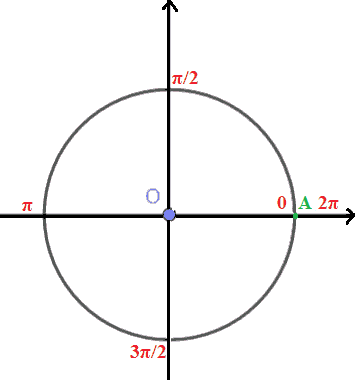
Notiamo che, i PUNTI nei quali la CIRCONFERENZA GONIOMETRICA INTERSECA gli ASSI CARTESIANI sono associati rispettivamente agli angoli di 0°, 90°, 180°, 270°, 360° che in radianti misurano rispettivamente 0, π/2, π, 3π/2, 2π.
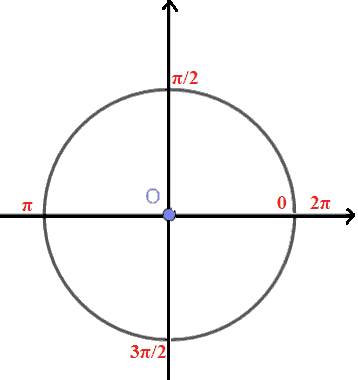
Chiaramente il punto A è associato sia all'angolo di 0 radianti che a quello di 2π radianti.