PROBLEMI CON GLI ANGOLI
- Gli angoli
- Angolo piatto, angolo giro e angolo nullo
- Angolo consecutivi e angoli adiacenti
- Somma di due angoli
- Differenza di due angoli
- Angolo retto - angolo acuto - angolo ottuso
- Angoli complementari, angoli supplementari, angoli esplementari
- Le unità di misura
- Sistemi di misura non decimali
In quest'ultima lezione dedicata agli ANGOLI vogliamo vedere come si risolvono alcuni PROBLEMI relativi agli angoli e le loro misure grazie alle nozioni apprese nelle lezioni precedenti.
Esempio 1:
Un angolo misura 30°: qual è l'ampiezza del suo complementare?
Per risolvere un problema di questo tipo è sufficiente sapere che due ANGOLI si dicono COMPLEMENTARI se la loro SOMMA è un ANGOLO RETTO.
Chiamiamo l'angolo di cui conosciamo l'ampiezza Alfa e chiamiamo il suo complementare Beta. Possiamo scrivere:
Alfa + Beta = Angolo Retto.
Ora noi sappiamo che l'angolo Alfa misura 30° e sappiamo anche che l'angolo retto è un angolo che misura 90°. Quindi possiamo scrivere:
30° + Beta = 90°.
Quindi se noi a 90° togliamo 30° sapremo quanto vale l'angolo Beta:
90° - 30° = 60° - ampiezza dell'angolo complementare.
Esempio 2:
Un angolo misura 30°: qual è l'ampiezza del suo supplementare?
Per risolvere un problema di questo tipo è sufficiente sapere che due ANGOLI si dicono SUPPLEMENTARI se la loro SOMMA è un ANGOLO PIATTO.
Chiamiamo l'angolo di cui conosciamo l'ampiezza Alfa e chiamiamo il suo supplementare Gamma. Possiamo scrivere:
Alfa + Gamma = Angolo Piatto.
Ora noi sappiamo che l'angolo Alfa misura 30° e sappiamo anche che l'angolo piatto è un angolo che misura 180°. Quindi possiamo scrivere:
30° + Gamma = 180°.
Quindi se noi a 180° togliamo 30° sapremo quanto vale l'angolo Gamma:
180° - 30° = 150° - ampiezza dell'angolo supplementare.
Esempio 3:
La differenza di due angoli adiacenti è di 100°. Calcolare le loro ampiezze.
Per risolvere un problema di questo tipo è sufficiente sapere che due ANGOLI si dicono ADIACENTI se la loro SOMMA è un ANGOLO PIATTO.
Chiamiamo i due angoli rispettivamente Alfa e Delta. Possiamo scrivere:
Alfa + Delta = 180°.
Alfa - Delta = 100°.
Ora risolviamo il problema aiutandoci con un grafico. Disegniamo i due angoli Alfa e Delta in modo che essi siano adiacenti:
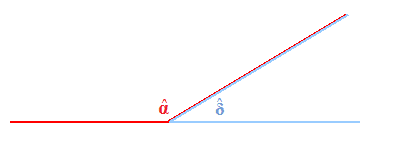
Sottraiamo all'angolo Alfa l'angolo Delta ed indichiamo l'angolo differenza con un tratteggio verde:
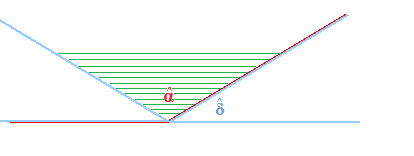
Ora possiamo osservare che l'angolo piatto è dato dalla somma di due volte l'angolo Delta (che abbiamo trattegiato con il colore azzurro) e dall'angolo differenza (trattegiato con il colore verde):
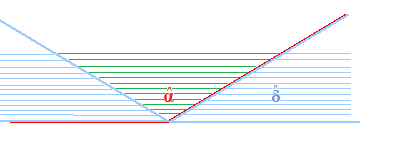
Poiché l'angolo piatto misura 180°, e poiché il nostro angolo differenza misura 100° possiamo scrivere:
180° - 100 = 2 volte l'angolo Delta
ovvero
80° = 2 volte l'angolo Delta
quindi Delta sarà:
80° : 2 = 40° - ampiezza dell'angolo Delta.
Noi sappiamo che la somma dell'angolo Alfa e dell'angolo Delta è pari a 180°, quindi se sottraiamo a 180° l'angolo Delta otteniamo l'angolo Alfa. Ovvero:
180° - 40° = 140° - ampiezza dell'angolo Alfa.






